Network Psychometrics

Alex LoPilato and Ben Listyg

Overview

Introduction to the network approach to psychometrics
Introduction to network analysis
Introduction to network (graphical) models

Modern Psychometric Methods

Latent Variable Models (IRT, CFA, EFA, etc.)
- Reflective models
- Formative models

Challenges with Latent Variable Models

Latent variable models do a poor job of specifying:
- The temporal precedence of the latent variable
- The causal response processes
- Causal associations among observed variables

The Network Approach

Discontent with current methods led a group of researchers to introduce and build on:
- Network theories of psychological phenomena
- Network (graphical) models

Network Theories: Constructs as Dynamical Systems

Reframe theories of psychological phenomena as a dynamic system of interactions among observable variables, which are referred to as autonomous causal entities.
Most network psychometric theories pull from the literature on dynamic systems and complex systems. An example is considering depression not as a construct, but as an attractor state of the depression system.

Network (Graphical) Models

Network psychometric analysis relies heavily on a class of statistical models called graphical models to estimate the network that underlies the observed variables.
One of the most common ways to estimate the underlying network is to use a model called the Gaussian Graphical Model, which is just a partial correlation matrix.

Network Analysis

What is a Network?

Networks (graphs) are mathematical objects that represent connections among different entities.
Mathematically, networks consist of a:
- Set of nodes or vertices
- Set of edges or links

Examples of Networks

Social Networks
Organizational Networks
Biological Networks
Information Networks

What is a Psychometric Network?

A psychometric network is a network in which the nodes are the observed variables and the edges are the conditional relationships among those observed variables.

Network Types

We can broadly categorize networks by the directionality (or lack thereof) and weights of the edges:
- Undirected vs Directed Networks
- Unweighted vs Weighted Networks
Psychometric network analysis typically deals with undirected and weighted networks.

Matrix Representation of a Network

The easiest way to mathematically manipulate a network is to turn it into a matrix. This matrix is referred to as an adjacency matrix.
Non-zero elements in the matrix represent connections between two nodes in the network.

Unweighted, Undirected Network

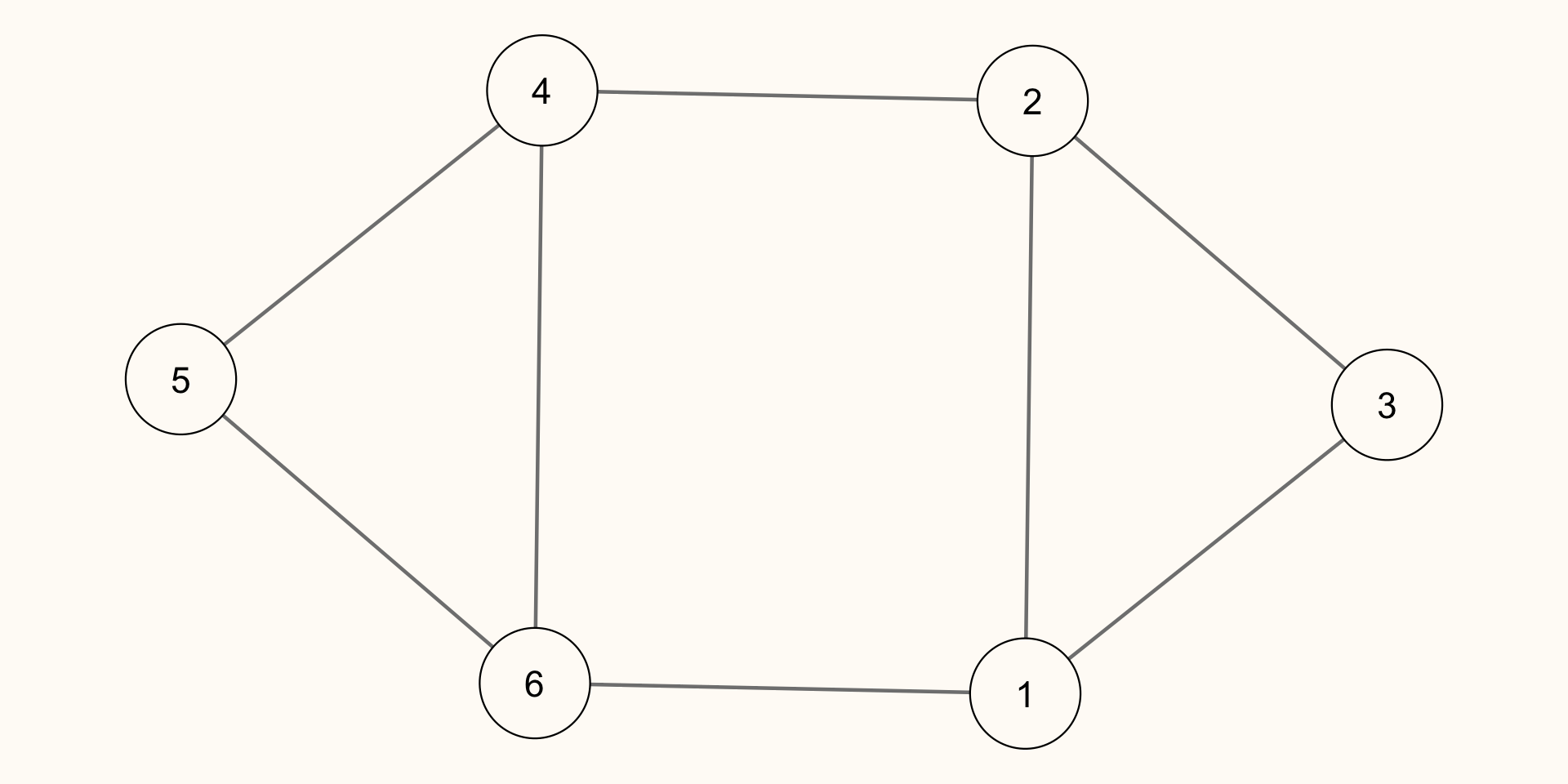
Adjacency Matrix

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    0    1    1    0    0    1
[2,]    1    0    1    1    0    0
[3,]    1    1    0    0    0    0
[4,]    0    1    0    0    1    1
[5,]    0    0    0    1    0    1
[6,]    1    0    0    1    1    0

Weighted, Unirected Network

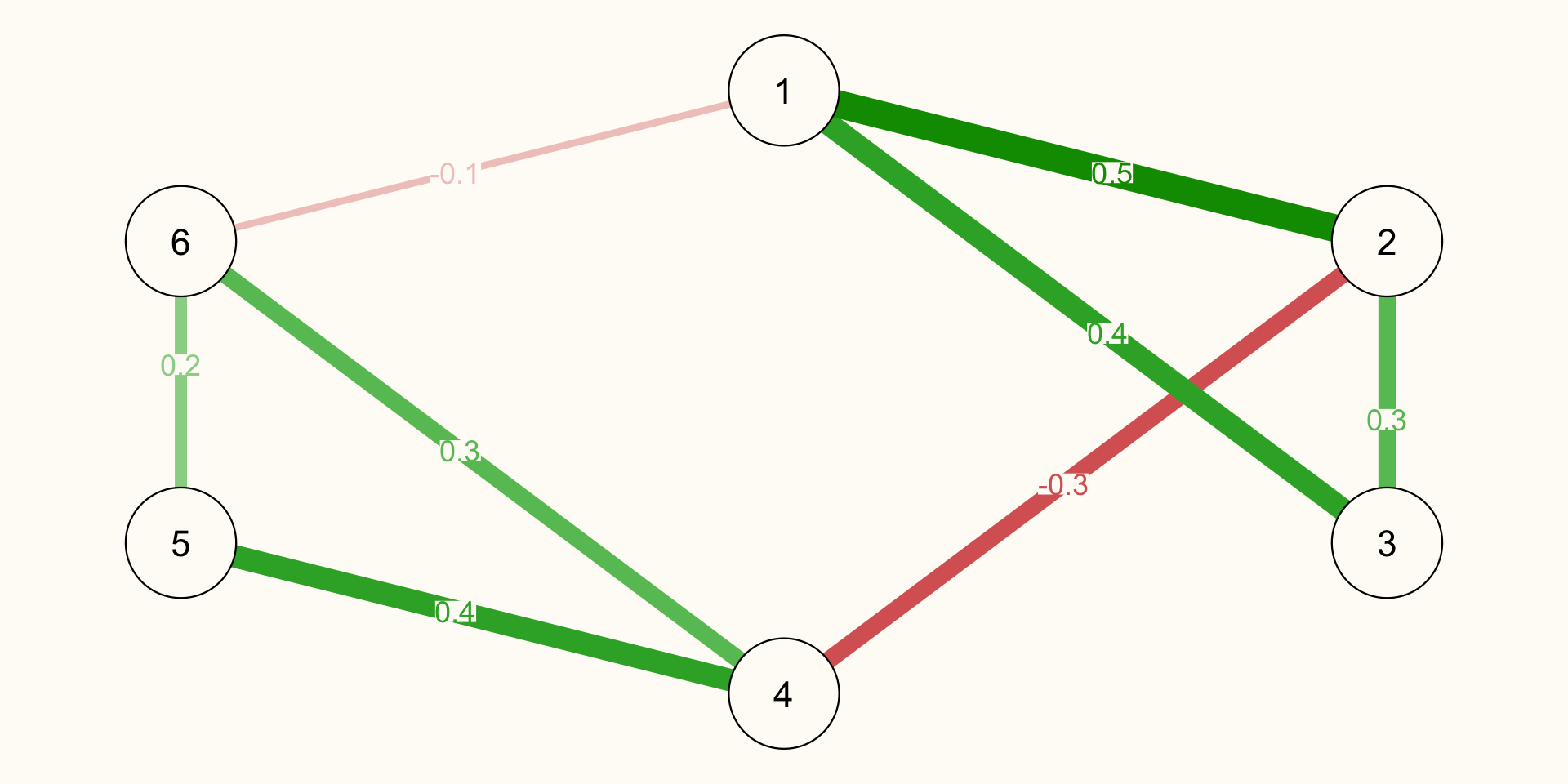
Weight Matrix

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  0.0  0.5  0.4  0.0  0.0 -0.1
[2,]  0.5  0.0  0.3 -0.3  0.0  0.0
[3,]  0.4  0.3  0.0  0.0  0.0  0.0
[4,]  0.0 -0.3  0.0  0.0  0.4  0.3
[5,]  0.0  0.0  0.0  0.4  0.0  0.2
[6,] -0.1  0.0  0.0  0.3  0.2  0.0

Analyzing Networks

Local network properties: Metrics focused on specific parts of a network
Global network properties: Metrics focused on the network as a whole

Local Network Properties: Centrality

Centrality is a class of network metrics that measure the importance of a given node by counting and, at times, weighting the number of direct or indirect connections a node has with other nodes.
Centrality metrics can be subdivided into:
- Direct connection centrality metrics
- Indirect connection centrality metrics

Direct Connection Centrality Metrics

Degree Centrality:

\[\sum_{j=1}^{n}{a_{ij}}\]

Strength:

\[\sum_{j=1}^{n}{\lvert w_{ij}\rvert}\]

Weighted Degree Centrality:

\[\sum_{j=1}^{n}{a_{ij}^{1-\alpha}\lvert w_{ij}\rvert^{\alpha}}\]

Expected Influence:

\[\sum_{j=1}^{n}{a_{ij}w_{ij}}\]

Direct Connection Centrality Example

rowSums(a) # Degree

[1] 3 3 2 3 2 3

rowSums(a*abs(w)) # Strength

[1] 1.0 1.1 0.7 1.0 0.6 0.6

rowSums(a*w) # Expected Influence

[1] 0.8 0.5 0.7 0.4 0.6 0.4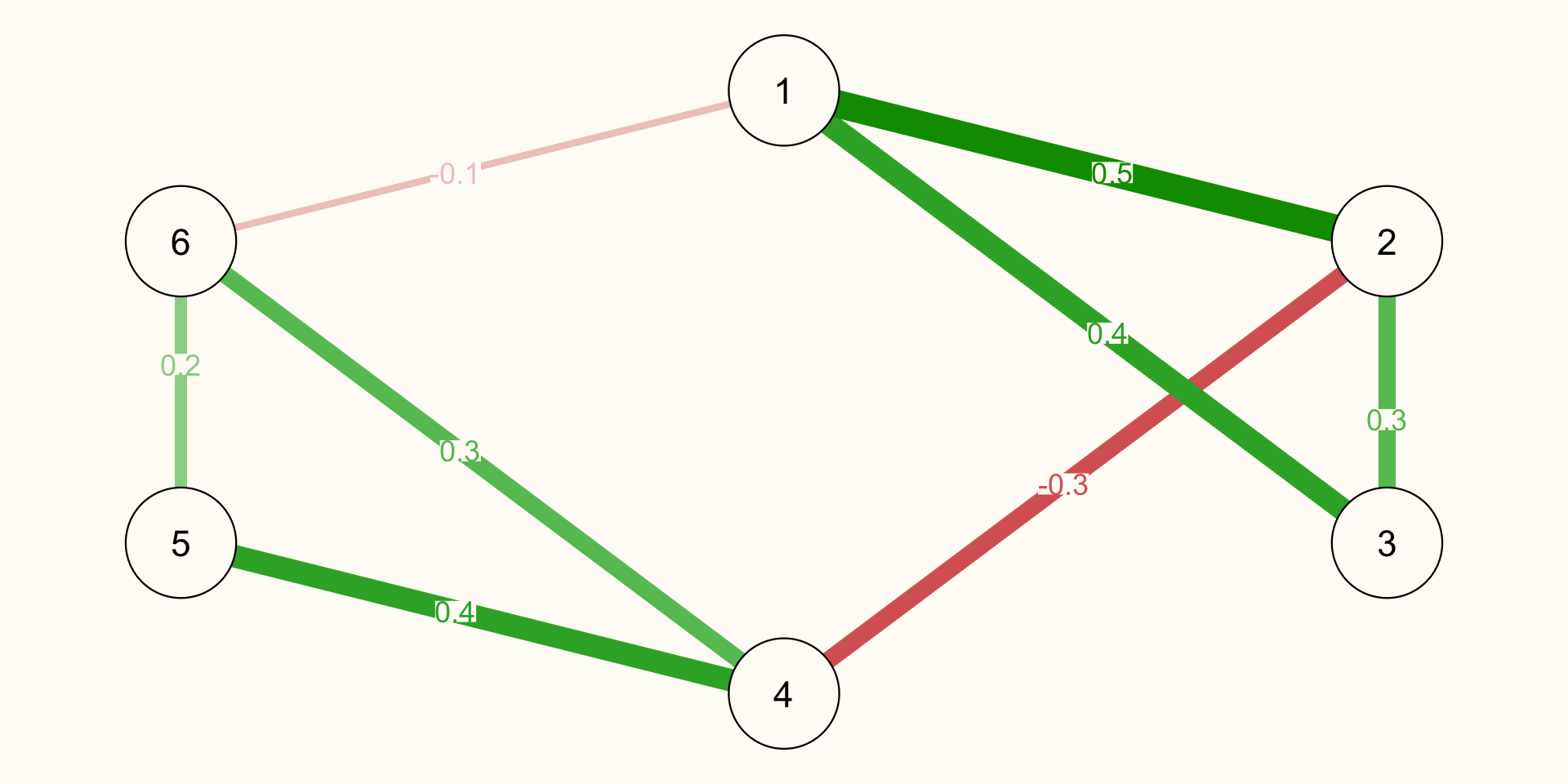

Direct Connection Centrality `qgraph` Example

qgraph::centralityPlot(w, include = c("Strength", "ExpectedInfluence"))

Path Metrics

Before we can calculate the indirect connection centrality metrics, we first need to understand path metrics:

Length: The distance between two nodes.

\[\text{Length}(i, j)=\frac{1}{\rvert w_{ij} \lvert^{\alpha}}\]

Distance: The shortest path between two nodes.

\[\text{Distance}(i, j)=min(w_{ik}+ \dots + w_{lj})\]

Indirect Connection Centrality Metrics

Closeness:

\[\frac{1}{\sum_{j=1}^{n}\text{Distance}(i,j)}\]

Betweeness:

\[\sum_{<j,k>}\frac{\text{# shortest paths from j to k that go through i}}{\text{# shortest paths between j and k}}\]

Expected Influence Two:

\[\sum_{j=1}^{n}a_{ij}w_{ij}+\sum_{j=1}^{n}a_{ij}w_{ij}\sum_{k=1}^{n}a_{jk}w_{jk}\]

Indirect Connection Centrality Example

(rowSums(w) + a%*%rowSums(w)) |> t()  # Expected Influence 2

     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]  2.4  2.4    2  1.9  1.4  2.2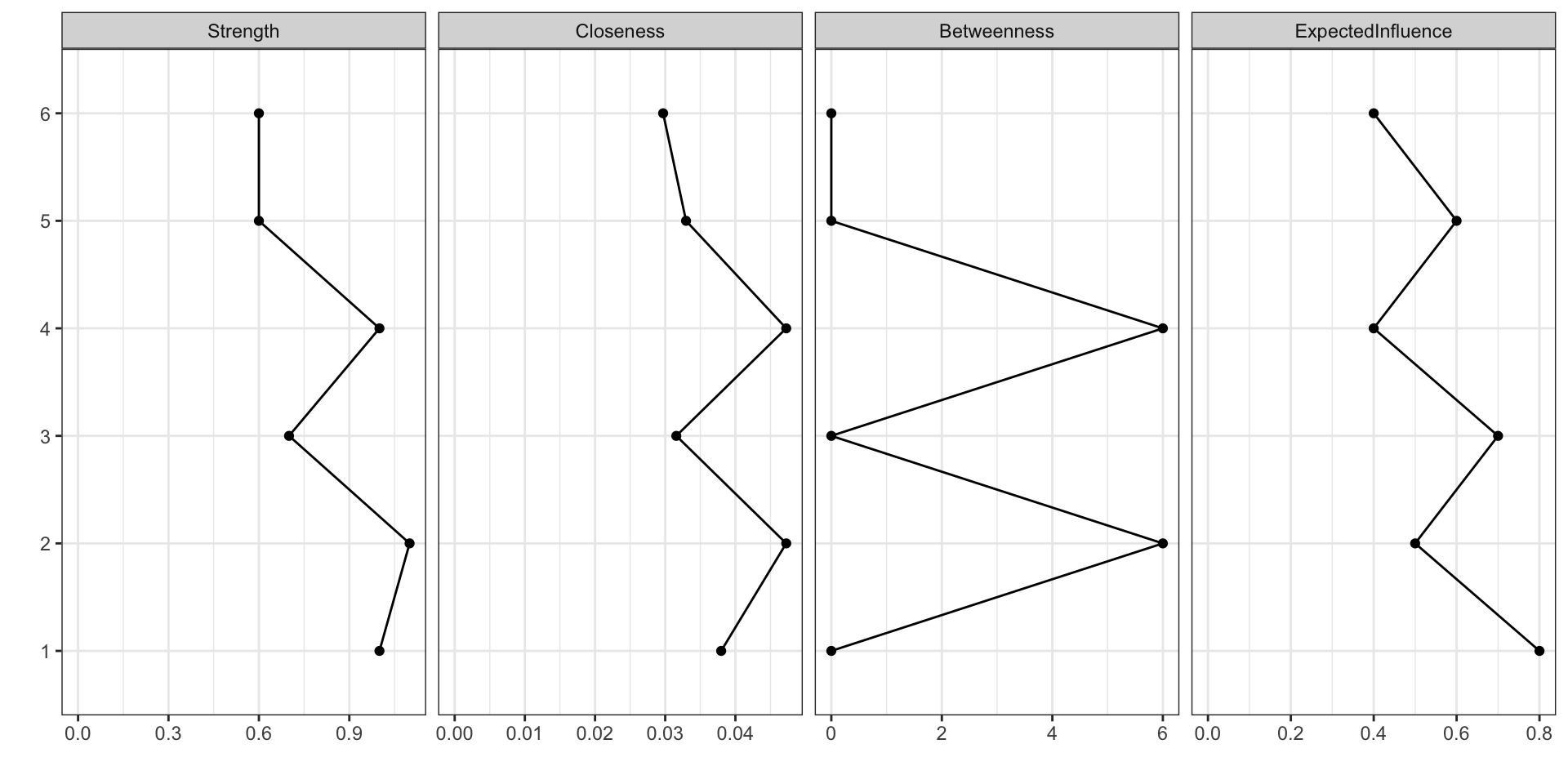

qgraph::centralityPlot(w, include = c("all"))

Local Network Properties: Clustering

Clustering is a metric that looks at how often two nodes that are connected to the same focal node are also connected to one another: the friend of my friend is also my friend.
I haven’t seen this used a whole lot in psychometric network analysis.

Global Network Properties: Density

It is often of interest to understand how connected your network is. This can be calculated using a network metric called density.

\[\text{Density}=\frac{\text{# Observed Edges}}{\text{# Possible Edges}}=\frac{\sum_{<i, j>}a_{ij}}{n(n-1)}\]

Global Network Properties: Small Worlds

Six degrees of Kevin Bacon
Small world network models are characterized by high clustering and short average path lengths–this does not happen when networks form completely at random.

Calculating Density and Small World Index in R

toy_graph <- qgraph::qgraph(w, DoNotPlot = TRUE) # Create your graph
toy_graph |> igraph::as.igraph() |> igraph::edge_density() # Calculate density

[1] 0.5333333

qgraph::smallworldIndex(toy_graph)$index # Calculate small world index

[1] 1.093175

Global Network Properties: Community Detection

In network analysis, community detection is a set of algorithms that attempt to find hidden communities within a network by identifying sets of nodes that have more connections among themselves than they have with other nodes outside of the set.
Common algorithms:
- Walktrap Algorithm
- Louvain Algorithm
- Fast-Greedy Algorithm

Community Detection Example

# Need to take the absolute value of the weighted network
toy_graph <- qgraph(abs(w), DoNotPlot = TRUE)
toy_graph |> igraph::as.igraph() |> igraph::walktrap.community()

IGRAPH clustering walktrap, groups: 2, mod: 0.33
+ groups:
  $`1`
  [1] 4 5 6
  
  $`2`
  [1] 1 2 3

Network Models

Network Psychometrics

In Part 1, you learned the theory and rationale and math of psychometric networks
In Part 2, we learn how to DO estimation of psychometric networks

Reminder from Part 1

Networks serve as an abstraction to represent the relationships (edges) between entities (nodes)
KEY!!!

Reminder from Part 1

Networks serve as an abstraction to represent the relationships (edges) between entities (nodes)
DISTINGUISHING!!!

Reminder from Part 1

Networks serve as an abstraction to represent the relationships (edges) between entities (nodes)
FACTOR!!!

Reminder from Part 1

In social networks, your data both nodes and edges that are observed
- Obvi there are more complex situations where you have missing data
  - Network missingness can be very tricky (Morrissett, 2013; Kossinets, 2006)
- This is neither time nor place for that though…

Reminder from Part 1

I/O context:
- Teams / Co-workers
Clinical:
- We can form a network between therapist and patients in group therapy setting (Koelhy & Shivy, 1998)
Developmental
- We can form a network of how babbies interact with other babbies (Cochran & Brassard, 1979)

Psychometric Networks

When do psychometric network analysis / using psychometric network models:
- All your nodes (items) are observed
- You are e s t i m a t i n g the relationships (edges) between nodes (items)

Psychometric Networks

When do psychometric network analysis / using psychometric network models:
- All your nodes (items) are observed
- You are e s t i m a t i n g the relationships (edges) between nodes (items)
How do we do that?

There are many paths to Rome

Start with a substantive question utilizing network theory (e.g. “I want to understand Construct X as a dynamic construct and/or complex system.”
1. Sachisthal et al. (2019)
  1. Scientific Interests Network - Psychometric network on student’s interest in science

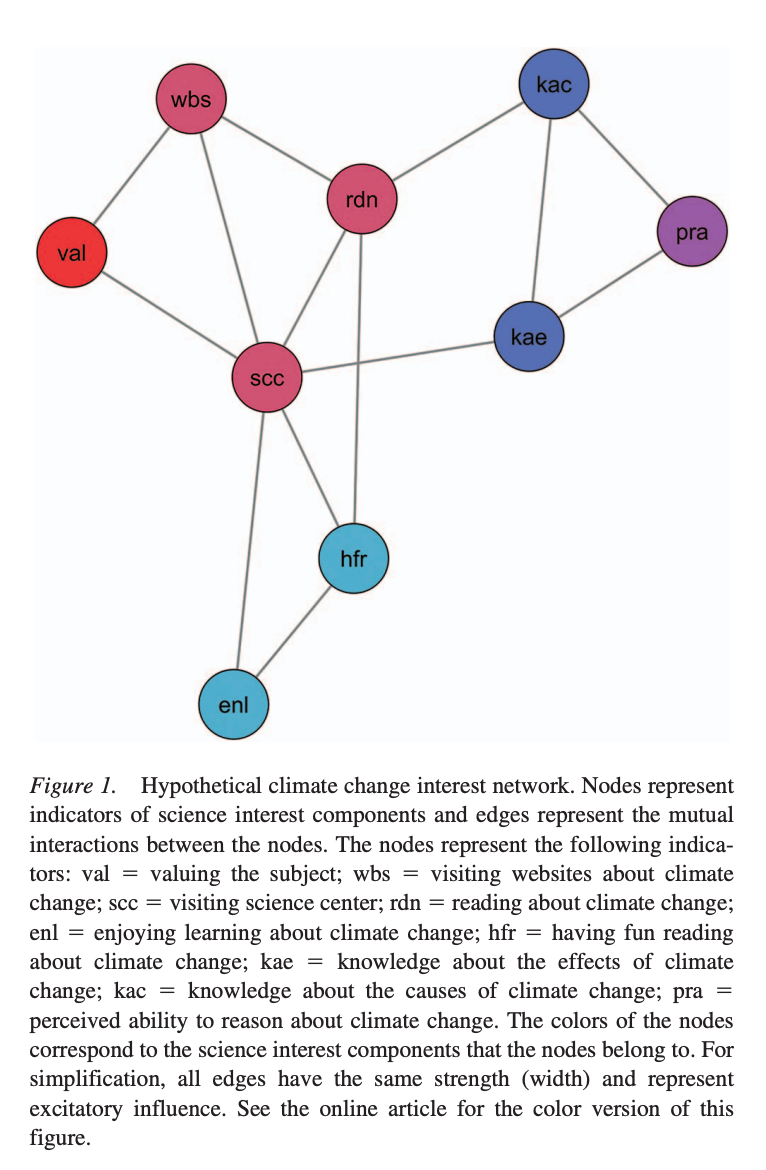
There are many paths to Rome

Theoretical perspectives on interests are all over the place.
Interests can potentially be conceptualized as “interacting indicators of interest components…indicators of affective, behavioral, and cognitive (including value and knowledge) components”
These indicators make up the variable of interest rather than being indicators of it
Provides new targets for interventions

There are many paths to Rome

Collect data
1. Research designs for network psychometrics can be:
  1. Longitudinal (e.g. EMA design; see Emorie Beck @ UC Davis for lots of examples of this)
  2. Cross-sectional
2. Sampling should be no different than any other psychological study

There are many paths to Rome

Analyze data

Time for F U N

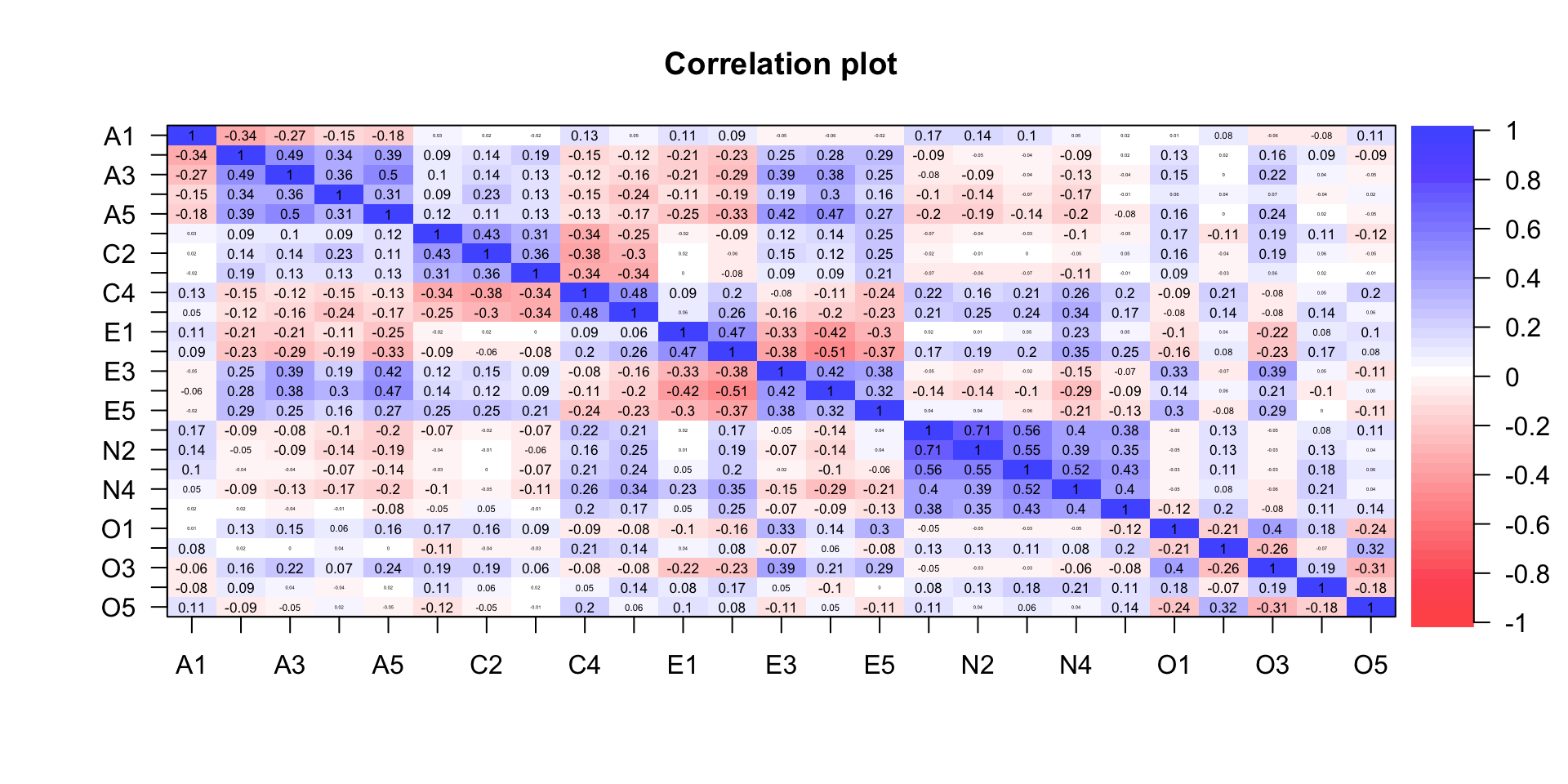
Analyzing Psychometric Network Data

We can do this with raw data OR correlation matrix

# First, we will load (or install first if you don't have it!) the qgraph AND the psych package:

library(qgraph)
library(psych)
library(dplyr) # Also loading this because I don't align with Alex's use of |> pipe

Analyzing Psychometric Network Data

# Next, let's examine our dataset

data("bfi")

glimpse(head(bfi))

Rows: 6
Columns: 28
$ A1        <int> 2, 2, 5, 4, 2, 6
$ A2        <int> 4, 4, 4, 4, 3, 6
$ A3        <int> 3, 5, 5, 6, 3, 5
$ A4        <int> 4, 2, 4, 5, 4, 6
$ A5        <int> 4, 5, 4, 5, 5, 5
$ C1        <int> 2, 5, 4, 4, 4, 6
$ C2        <int> 3, 4, 5, 4, 4, 6
$ C3        <int> 3, 4, 4, 3, 5, 6
$ C4        <int> 4, 3, 2, 5, 3, 1
$ C5        <int> 4, 4, 5, 5, 2, 3
$ E1        <int> 3, 1, 2, 5, 2, 2
$ E2        <int> 3, 1, 4, 3, 2, 1
$ E3        <int> 3, 6, 4, 4, 5, 6
$ E4        <int> 4, 4, 4, 4, 4, 5
$ E5        <int> 4, 3, 5, 4, 5, 6
$ N1        <int> 3, 3, 4, 2, 2, 3
$ N2        <int> 4, 3, 5, 5, 3, 5
$ N3        <int> 2, 3, 4, 2, 4, 2
$ N4        <int> 2, 5, 2, 4, 4, 2
$ N5        <int> 3, 5, 3, 1, 3, 3
$ O1        <int> 3, 4, 4, 3, 3, 4
$ O2        <int> 6, 2, 2, 3, 3, 3
$ O3        <int> 3, 4, 5, 4, 4, 5
$ O4        <int> 4, 3, 5, 3, 3, 6
$ O5        <int> 3, 3, 2, 5, 3, 1
$ gender    <int> 1, 2, 2, 2, 1, 2
$ education <int> NA, NA, NA, NA, NA, 3
$ age       <int> 16, 18, 17, 17, 17, 21

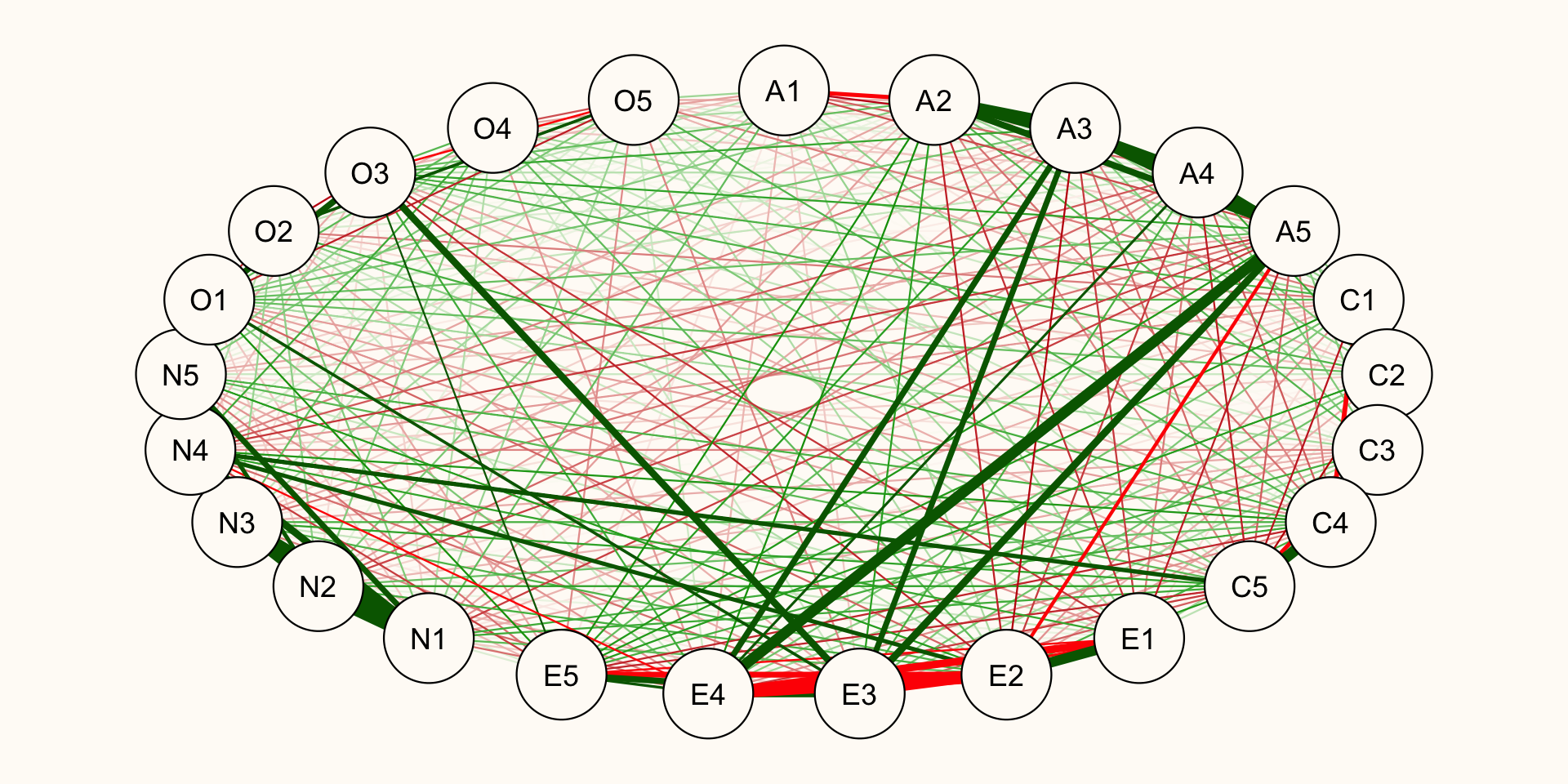
Analyzing Psychometric Network Data

The previous network was an unregularized

This means all edges were estimated, even super tiny ones
But, what happens if we ~ regularize ~ it?

Analyzing Psychometric Network Data

Quick aside:

What is regularization?

A process of “shrinking” tiny values towards zero.

Analyzing Psychometric Network Data

What we can see is that the correlation matrix is much more “sparse”
There are substantially more 0’s all over the place and the previously bigger values are smaller than before.

Analyzing Psychometric Network Data

What does this regularized network look like?

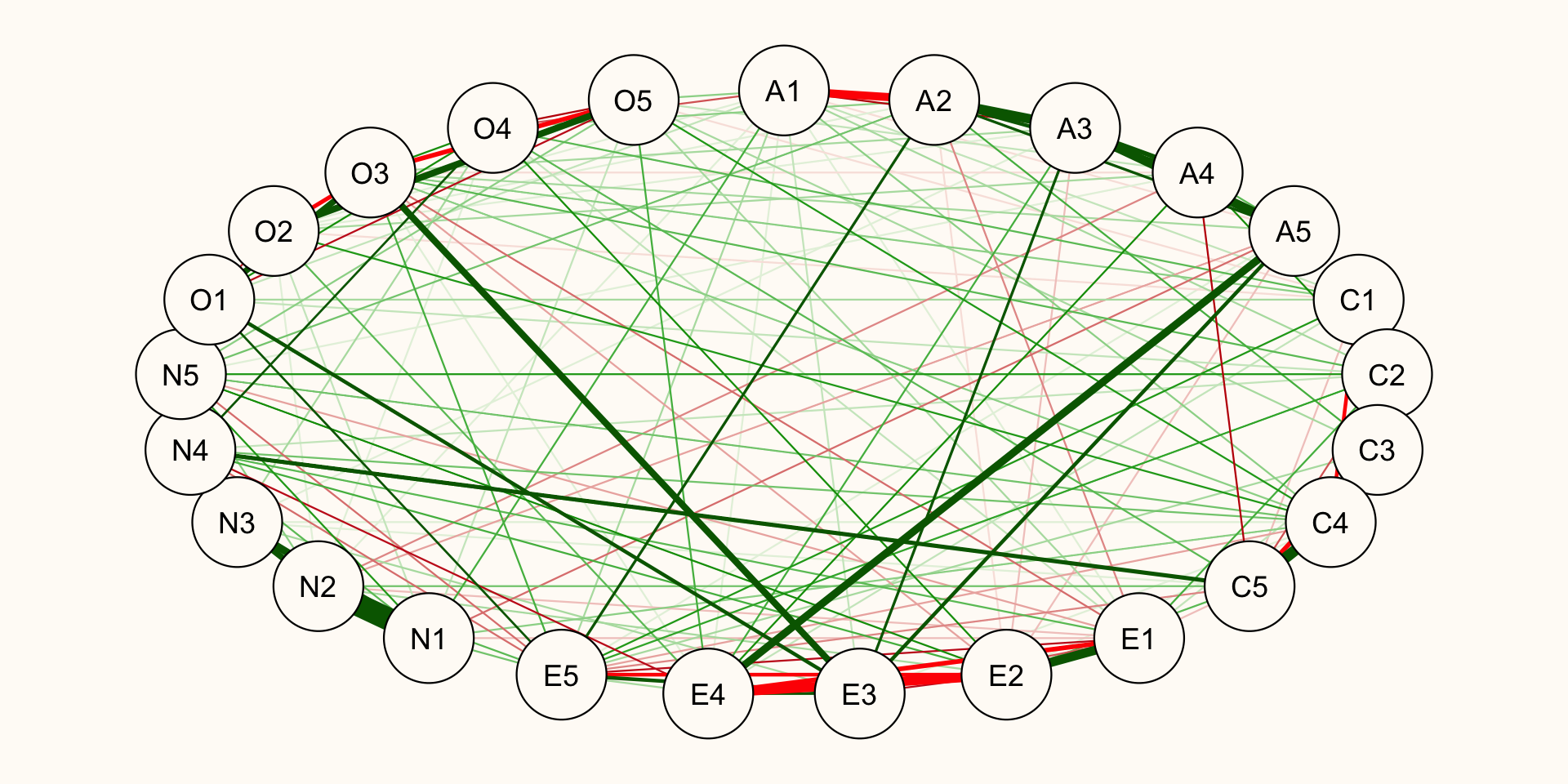
Analyzing Psychometric Network Data

Why do we regularize?

Separating signal from noise
We know everything is (to a degree) correlated with everything
Regularization helps siphon the signal from the noise and what’s left over is “truth” and aid with selecting the “true” model.

Analyzing Psychometric Network Data

Now that we’ve estimated a psychometric network… what can we do?

1) Estimate global network properties

2) Estimate individual node properties

Analyzing Psychometric Network Data

1) Estimate global network properties

Example: Smallworldness

Substantive value: Lots of networks have smallworld properties (see Jonathan Kleinberg or Aaron Clauset’s work on this for example of small-world networks all over the place). A smallworld network implies any two nodes in the network can reach each other through a short sequence of other nodes (Kleinberg, 2001)

Daleage et al. (2016) demonstrate that attitudinal networks display smallworld characteristics

Carter et al. (2020) demonstrate the utility of smallworld networks for predicting turnover

                             .
smallworldness       1.0313728
trans_target         0.5317888
averagelength_target 1.4800000
trans_rnd_M          0.5156428
trans_rnd_lo         0.4913712
trans_rnd_up         0.5414952
averagelength_rnd_M  1.4800867
averagelength_rnd_lo 1.4800000
averagelength_rnd_up 1.4833333

Analyzing Psychometric Network Data

2) Estimate individual node properties

   Betweenness   Closeness
N4          72 0.002830050
N3          62 0.002534412
C5          57 0.002721057
E4          54 0.002948168
A3          48 0.002689122
A2          46 0.002580368

Analyzing Psychometric Network Data

Additional things you can do with networks:

Community Detection
- Do different nodes “hang out” together?

Analyzing Psychometric Network Data

Network Comparison Test (NCT)
- Do different groups have the same / different network structures?
- BIG open area for research imo
  - Lots of existing work on graph comparisons in CS / Stats
  - How does it translate to psychometric data?
    - Cosma Shalizi is prolific in this space

Some Critiques of Psychometric Network Analysis

Model Selection: Are network models appropriate for psychological data?
Study Design: Can we infer anything about a dynamical system from cross-sectional data?
Estimation Reliability: How stable/replicable are psychometric networks?
Interpretation of Measures: Can we even interpret network metrics applied to psychometric networks?

Network Psychometrics

Overview

Modern Psychometric Methods

Challenges with Latent Variable Models

The Network Approach

Network Theories: Constructs as Dynamical Systems

Network (Graphical) Models

Network Analysis

What is a Network?

Examples of Networks

What is a Psychometric Network?

Network Types

Matrix Representation of a Network

Unweighted, Undirected Network

Adjacency Matrix

Weighted, Unirected Network

Weight Matrix

Analyzing Networks

Local Network Properties: Centrality

Direct Connection Centrality Metrics

Direct Connection Centrality Example

Direct Connection Centrality qgraph Example

Path Metrics

Indirect Connection Centrality Metrics

Indirect Connection Centrality Example

Local Network Properties: Clustering

Global Network Properties: Density

Global Network Properties: Small Worlds

Calculating Density and Small World Index in R

Global Network Properties: Community Detection

Community Detection Example

Network Models

Network Psychometrics

Reminder from Part 1

Reminder from Part 1

Reminder from Part 1

Reminder from Part 1

Reminder from Part 1

Reminder from Part 1

Psychometric Networks

Psychometric Networks

There are many paths to Rome

There are many paths to Rome

There are many paths to Rome

There are many paths to Rome

There are many paths to Rome

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Analyzing Psychometric Network Data

Some Critiques of Psychometric Network Analysis

Direct Connection Centrality `qgraph` Example